Constraint-based Syntax 2: Week 2

The Argument Realization Principle (ARP)

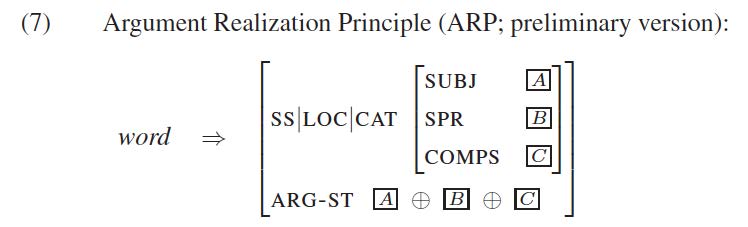
Recall that in GS the syntactic arguments of a word are in a sense represented twice: once on the ARG-ST (argument structure) list which, among others, is used for Binding Theory, and again on one of the valence lists SUBJ, SPR, and COMPS. Rather than being arbitrary, the relationship between the ARG-S and the valence lists is governed by the Argument Realization Principle:

In words, the principle says that the ARG-ST list is the result of merging the three valence lists into one list, with the elements of the SUBJ list coming first, followed by the elements on the SPR list, followed by the elements on the COMPS list.

Besides the ARP, the valence properties of words depend on their part of speech. Thus, all words of part of speech v must have a SUBJ list with exactly one element on it and a SPR list which is empty. In combination with the ARP, verbs of part of speech v thus must have the following properties:

1. The ARG-ST must have at least one element on it.
2. The first element of the ARG-ST is also the single element on the SUBJ list.
3. If there are additional elements on the ARG-ST, then these elements also occur on the COMPS list.
4. The elements which appear both on the ARG-ST and the COMPS list, appear in the same order on both lists.

The following Exercises on the append relation have the purpose of showing that the 4 statements above must be true.

Exercises on the Argument Realization Principle

Head Features

GS postulate the following head features:

Part of speech	Supertypes	Feature	Value type	Encoding function
verbal	subst	VFORM	vform	verb form
		IC	boolean	independent clause
verb	verbal, subst	AUX	boolean	auxiliary construction

     subst pred:bool mod:mod_synsem mod_label:label

           verb aux:bool pol:bool inv:bool
              v
              g
           c
        a deg:bool
        adv  
           pol_adv neg:bool
        nominal
           p pform:pform
           n case:case
     func spec:sem_obj 
        d
        deg_adv % not in the book

  ↑ Main page         ↑ Week 1